Mathematische Ostereier-Suche: Welche Zahlen verstecken sich hinter den bunten Eiern?

Bevor die Ostereier-Suche so richtig losgeht, gibt es erst mal Osterbrot und Frühstückseier. Mit einem Mathelehrer im Haus gestaltet sich bereits das perfekte Frühstücksei zu einer Rechenaufgabe, doch zunächst muss der Wert der Eier bekannt sein.

Während sich am Frühstückstisch Gewicht, Luftdruck und gewünschter Härtegrad der Eier auf die Kochzeit des perfekten Eis auswirken, geht es in diesem Rätsel „nur“ um Zahlen. Können Sie sagen, welche Zahlen sich hinter den bunten Eiern verstecken?

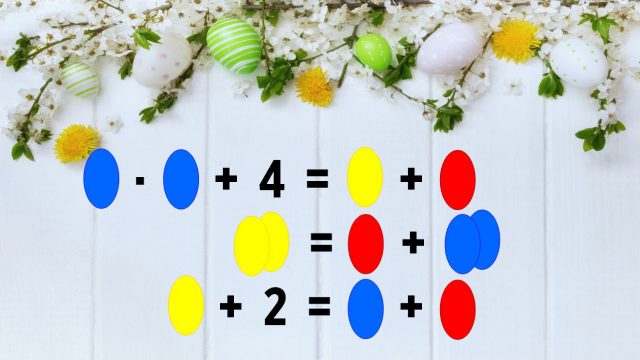
Bunte Ostereier stehen für unterschiedliche Zahlen, aber welche? Foto: ts/Epoch Times

Ohne große Umwege – denn Sie wollen entweder frühstücken oder Eier suchen – widmen wir uns der (ersten) Lösung. Auch wer mit der Mathematik auf Kriegsfuß steht und auch keine Kinder hat, die sich auf eine Matheprüfung vorbereiten müssen, findet mit ein bisschen Glück die Werte der Eier heraus.

Probieren geht über Studieren

Die einfachste Möglichkeit, die Zahlen hinter den Eiern zu finden, ist durch Probieren. Da bunte Eier zwar hübsch aussehen, aber mathematisch keine Bereicherung sind, ist es zunächst empfehlenswert den „Eiersalat“ in mathematische Gleichungen umzuwandeln.

Natürlich können Sie beliebige Variablen für blaue, rote und gelbe Eier einsetzten. Um die Lösung hinterher einfacher zuordnen zu können, nutzen wir B für blaue Eier, R für rote Eier und G für gelbe Eier. Achtung: Bei der zweiten Gleichung sind jeweils zwei gelbe und zwei blaue Eier zusammengefasst:

(I)        B · B + 4 = G + R
(II)           G + G = R + B + B     oder     2G = R + 2B
(III)          G + 2 = B + R

Um den mathematischen Rechenregeln Genüge zu tun, ist es ratsam, zuerst das Produkt zu vereinfachen. Durch Probieren und Einsetzten von B = 0 fällt das Produkt sogar ganz weg und die Gleichungen vereinfachen sich wie folgt:

(I)                4 = G + R
(II)            2G = R
(III)      G + 2 = R

Nach dem Einsetzen der dritten Gleichung in die Erste ergibt sich 4 = G + (G + 2). Daraus folgt 4 = 2G + 2, durch Umstellen ergibt sich 2 = 2G und schließlich der Wert des gelben Eis mit 1. Anhand Gleichung (I) muss das rote Ei für eine 3 stehen. Das jedoch beißt sich mit der zweiten Gleichung und daraus folgt, dass das blaue Ei tatsächlich existiert und nicht null ist.

Probieren bis der Osterhase kommt

Notorische Mathemuffel probieren als nächstes B = 1, und sollte das nicht passen B = 2.

Für B = 1 zeigt sich:

(I)               5 = G + R
(II)           2G = R + 2
(III)     G + 2 = 1 + R

Aus (II) und (III) lässt sich G = 3 und R = 4 berechnen, das widerspricht wiederum der ersten Gleichung. Damit ist B größer als 1.

Für B = 2 lauten die Gleichungen:

(I)               8 = G + R
(II)           2G = R + 4
(III)     G + 2 = 2 + R

Gleichung (III) besagt G = R, damit folgt aus (I) 8 = 2G und G = R = 4. Die zweite Gleichung bestätigt die Lösung. Das rote und gelbe Ei ist 4 Zähler wert, das blaue Ei 2.

Quadratische Gleichungen haben keine, eine oder zwei Lösungen

Beim Blick auf die erste Gleichung könnte dem Eierkoch etwas auffallen. Das Produkt aus zwei blauen Eiern ist ein blaues Quadrat-Ei. Da quadratische Eier (Gleichungen) mehr als eine Lösung haben können, müssen Sie wohl oder übel doch noch weiter rechnen.

Zusammenfassen und Umformen der Gleichungen ergibt:

(I)        B² + 4 – G = R
(II)          2G – 2B = R
(III)       G + 2 – B = R

Setzten wir nun die zweite Gleichung mit den anderen gleich, verschwinden die roten Eier und eine Gleichung. Übrig bleibt zunächst:

(I)        B² + 4 – G = 2G – 2B
(II)        G + 2 – B = 2G – 2B

Und nach weiterem Umformen:

(I)        B² + 2B + 4 = 3G

Daraus können wir schließlich B² – 2B + 4 = 3 · (B + 2) schreiben und für die quadratische Lösungsformel nach 0 umstellen. Dann erhalten wir:

(I)‘            B² + 2B + 4 = 3 · (B + 2)
(I)“             B² – B + 4 = 6
(I)“‘            B² – B – 2 = o

Die quadratische Lösungsformel bestätigt die oben genannte Lösung B₁ = 2; G₁ = R₁ = 4 und erweitert sie um die zweite Lösung B₂ = -1; G₂ = 1; R₂ = 4.

Da uns negative Eier öfter selbst in die Pfanne hauen als andersherum, gehen wir schnell zu nächsten Aufgabe, denn eine kräftige Farbe fehlt noch bei dieser mathematischen Ostereier-Suche: Grün.

Welchen Wert hat das grüne Ei?

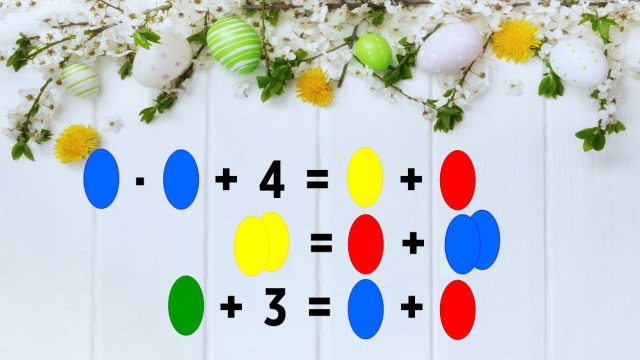
Grüne Eier sollte man besser nicht mehr essen. Foto: ts/Epoch Times

Mit dem zusätzlichen grünen Ei wird das Gleichungssystem tatsächlich unlösbar, sodass Probieren die einzige Möglichkeit scheint. Wer jedoch genau nachdenkt und sich neben den mathematischen Grundlagen auch an die künstlerischen Grundlagen aus der Schule erinnert, findet eine andere – mathematisch saubere – Lösung.

Grün ist in der sogenannten „subtraktiven“ Farbmischung des Kunstunterrichts die Mischfarbe aus Gelb und Blau, sozusagen der Durchschnitt. Zurück bei der mathematischen Eiersuche ergibt sich daraus eine vierte Gleichung GRün = (GElb + Blau) : 2 beziehungsweise Gr = (Ge + B) : 2.

(I)        B · B + 4 = G + R
(II)           G + G = R + B + B     oder     2G = R + 2B

Nach Einsetzten von (IV) in (III) und einigen Schritten des Umformens, Gleichsetzten und noch mehr Umformen ergibt sich schließlich B² – B – 2 = o mit denselben Lösungen wie oben.

Das grüne Ei bildet – wie im Kunstunterricht gelernt – den Mittelwert zwischen blauen und gelben Eiern. Aus B₁ = 2 und  Ge₁ = 4  ergibt sich Gr₁ = 3 und aus B₂ = -1 und Ge₂ = 1 ergibt sich Gr₂ = 0. In beiden Fällen sind sowohl die mathematischen als auch die künstlerischen Bedingungen erfüllt und es gibt keinen Ostereier-Salat.

Wer in Kunst (und Informatik) genau aufgepasst hat, erinnert sich vielleicht dunkel an die additive Farbmischung. In dieser ist Grün eine der drei Hauptfarben und aus Grün und Rot entsteht Gelb.

Irrationale Ostereier im Kunst- und Informatikunterricht

Nehmen wir wiederum Gelb als Mittelwert von Rot und Grün an, lautet die vierte Gleichung Ge = (R + Gr) : 2 und durch Umstellen Gr = 2Ge – R. Das können wir nun in die dritte Gleichung einsetzten und erhalten:

(I)                 B² + 4 = Ge + R

Der weitere Lösungsweg ergibt sich analog zur obigen Berechnung und führt zur finalen Gleichung 2B² – 5B – 1 = o. Die Anwendung der Lösungsformel beinhaltet dann die Wurzelberechnung B_1/2 = 2,25 ± √25/16 + 8/16. Die Wurzel von 33 ist jedoch irrational und damit hat (mindestens) das blaue Ei einen Knacks weg. Kaputte Eier sollte man (ebenso wie grüne) lieber entsorgen. Also schnell zur letzten Lösung.

Anders als die Farbmischung im Kunstunterricht addiert der Informatiker die Farbwerte eigentlich. Daraus leitet sich als vierte Gleichung Ge = Gr + R ab. Aus

(I)               B² + 4 = Ge + R
(II)                2Ge  = R + 2B
(III)    Ge – R + 3 = B + R

ergibt sich wiederum B² – B + 1 = o. Das mathematisch geschulte Auge rennt jetzt sofort zur Alarmglocke, denn der resultierende Wurzelterm in der Lösungsformel ist negativ. Negative Wurzeln gibt es in der Schulmathematik nicht, ein Mathelehrer weiß sich jedoch mit imaginären Zahlen zu helfen – Die Wurzel von minus Eins lautet daher „i“.

Die mathematische Ostereier-Suche endet also entweder mit negativen, irrationalen oder imaginären Eiern. Bevor die Mathematik Sie übermannt, schlagen Sie die Eier lieber in eine Pfanne und genießen Sie die Spiegeleier. Guten Appetit und viel Erfolg bei der Ostereier-Suche!