
Rätsel für Querdenker: Verbinden Sie diese Punkte mit vier (oder weniger) geraden Linien

Egal, ob sie im Büro sitzen oder am Fließband stehen, viele Menschen haben den immer gleichen Tagesablauf. Für einen Blick über den Tellerrand, kreative Arbeit oder Querdenken bleibt wenig Gelegenheit. Höchste Zeit diese Punkte nachzuholen.
Bei so viel Zeit im Job ist es wenig verwunderlich, dass Kinder oft schneller die Lösung eines Rätsels finden. Doch je komplexer die Lösung wird, desto mehr ist die Erfahrung auf der Seiten der „Großen“.
Das folgende Rätsel enthält alles. Kleine und große Rätselfreunde kommen hierbei auf ihre Kosten – und alles, was Sie dafür brauchen, sind ein Stift und ein Blatt Papier.
Verbinden Sie diese neun Punkte mit vier geraden Linien
Die heutige Aufgabe lautet: Verbinden Sie neun, in einem 3 x 3-Quadrat angeordnete Punkte mit vier geraden Linien. Die Schwierigkeit besteht darin, dass Sie den Stift erst am Ende der vierten Linie wieder vom Papier heben dürfen.
Sie sagen das ist einfach? Dann legen Sie los! – Und wenn Sie damit fertig sind, suchen Sie nach einer Lösung mit drei, zwei oder gar einer Linie.

Können Sie diese neun Punkte mit vier geraden Linien verbinden, ohne den Stift abzusetzen? Foto: ts/Epoch Times
Während bei dieser Aufgabe (noch) die Kinder im Vorteil sind, stehen viele Erwachsene vor demselben Problem. Fünf Linien, begonnen in einer Ecke und in Form einer Spirale, verbinden die Punkte ohne Probleme, aber wie soll das mit vier gehen?
Ein Blick über den Tellerrand offenbart die Lösung
An diesem Punkt müssen wir zugeben, dass es innerhalb des 3 x 3-Quadrats tatsächlich keine Lösung gibt. Die Lösung erfordert einen Blick über den berühmten Tellerrand – oder, wenn die Punkte sehr groß gezeichnet sind, eine Linie über den Rand des Blattes.
Durch das Erweitern des Musters entstehen neue Möglichkeiten, neun (oder mehr) Punkte zu verbinden. So umfasst die Lösung mit vier geraden, ununterbrochenen Linien in Wahrheit nicht nur neun, sondern sogar elf Punkte.
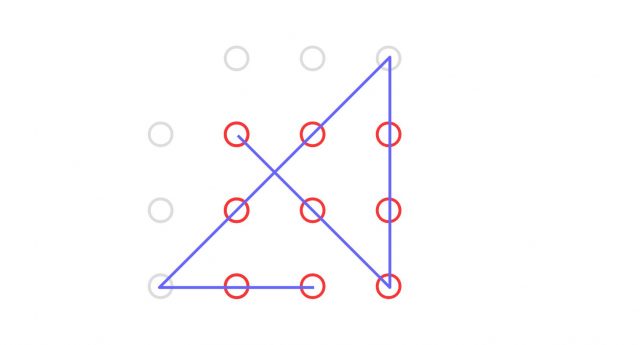
Vier Gerade Linien, die über den „Tellerrand“ hinausreichen, verbinden alle neun Punkte. Foto: ts / Epoch Times
Wer jetzt glaubt, dass eine Lösung mit nur drei Linien unmöglich sei, sollte die Herausforderung bis zum Maximum annehmen und weiter über den Tellerrand schauen. Um die neun Punkte mit einer Linie weniger zu verbinden, braucht man in der Tat viel mehr Platz – und darf kein Mathematiker sein.
Neun Punkte, drei Linien
In der Mathematik ist ein Punkt ein Objekt „ohne jede Ausdehnung“, sodass bereits ein Bleistiftpunkt die Definition sprengt. Unter der Voraussetzung das die Punkte eine Ausdehnung haben – und damit eher Kreise sind – ist das Rätsel auch mit drei geraden, ununterbrochenen Linien lösbar.
Sobald die Linien nicht die Mittelpunkte der „Punkte“ berühren müssen, können sie etwas schief verlaufen. Durch den Winkel zwischen der Geraden der Mittelpunkte und den Linien scheiden sie sich in einem Punkt irgendwo am Blattrand. Das ermöglicht eine dreiteilige Zickzack-Linie, die wiederum alle neun Punkte verbindet.
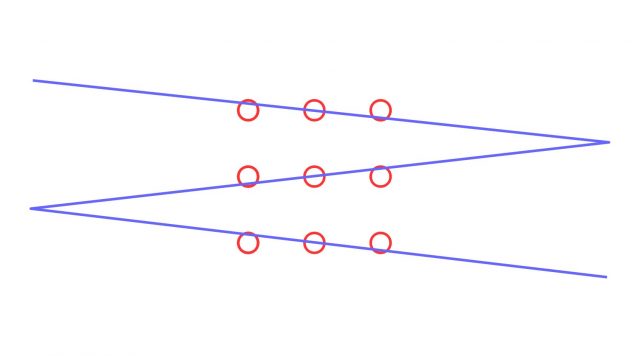
Wenn die Punkte nicht im Mittelpunkt berührt werden müssen – und das Blatt groß genug ist – reichen auch drei Linien. Foto: ts / Epoch Times
Während Kinder die erste Lösung oft schneller finden als Erwachsene, brauchen sie für die Lösung mit drei Linien oft länger als ihre Eltern. Die nächste Herausforderung wiederum – die Lösung mit nur zwei Linien – könnten jedoch schon die kleinsten Künstler finden. Unabsichtlich.
Mit zwei Linien zurück auf den Rätsel-Teller
Genug vom über den Tellerrand schauen, zurück zu den eigentlichen 3 x 3 Punkten. Auch bei der Lösung mit zwei Linien gelten dieselben Bedingungen wie zuvor: gerade Linien und ohne Absetzen. Aber niemand hat gesagt, dass Sie den Stift nicht wechseln dürfen …
Um alle Voraussetzungen zu erfüllen, nehmen Sie jetzt den dicksten Filzstift, den Sie finden können. Falls Sie eine Werkstatt in der Nähe haben, tut es ein breiter Pinsel und ein Eimer Farbe ebenso.
Ähnlich wie in der vorigen Lösung, schneidet die Linie nun nicht mehr die Mittelpunkte, dafür ist die „Linie“ hoffentlich so dick, dass sie gleich zwei Reihen Punkte anschneidet. Am Ende wird der Filzstift oder Pinsel auf die andere Seite geklappt und mit der Rückseite ein zweiter Farbbalken gezogen.
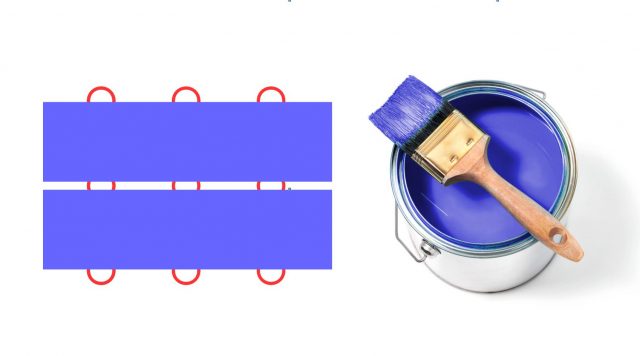
Um alle Punkte mit nur zwei Linien zu verbinden, muss der „Stift“ breiter werden. Foto: ts / Epoch Times
Sollten sich die Punkte in kindlicher Reichhöhe an der Wand befinden, könnte ein kleiner Künstler auch aus Versehen auf diese Lösung stoßen. Und für die Lösung mit nur einer Linie? Wir behaupten kühn, dass Ihre Kinder zumindest eine Möglichkeit nicht finden.
Mit Bleistift in die dritte Dimension
Natürlich könnte ein noch breiterer Pinsel alle neun Punkte auf einmal überstreichen, doch wie bisher soll jede Lösung einzigartig sein. Ein XXL-Pinsel gilt nicht, denn für die Lösung mit nur einer Linie reicht auch der Stift aus den ersten beiden Lösungen.
Der Trick liegt jedoch in der dritten Dimension und spätestens jetzt sollten Sie die neun Punkte auf Papier statt auf den Monitor malen – der lässt sich so schlecht biegen.

Neun Punkte kann man nicht mit einer geraden Linie verbinden … Foto: ts / Epoch Times

… oder etwa doch? Foto: ts / Epoch Times
Der Sprung in die dritte Dimension geht nicht nur weit über den Tellerrand hinaus, sondern erfordert einen ganzen Stapel an Tellern.
Wickelt man um diese Teller nun eine Schnur oder eine gedachte gerade Linie ergibt sich eine Spirale. Auf dieser Spirale liegen alle neun Punkte.

Rollt man das Blatt Papier schräg zusammen, liegen alle neun Punkte auf einer (spiralförmigen) Linie. Foto: ts / Epoch Times
Das gerollte Papier ermöglicht, die Spirale auf zweierlei Art als gerade Linie zu zeichnen. Einerseits können Sie den Stift an ein Lineal anlegen und um die Rolle „wickeln“, andererseits könnten Sie die Papierrolle drehen und entlang der Mittelachse langsam einen Strich ziehen.
Nur dreidimensional lösbar
Durch die Drehung entsteht in beiden Fällen aus der Linie eine Spirale, die alle neun Punkte miteinander verbindet. Erst zurück in der zweiten Dimension zerfällt die Spirallinie in drei Teile.
Die Bruchstücke zeigen jedoch, dass die Linie tatsächlich gerade ist und dass, solange Sie ausreichend genau rollen und zeichnen können, diese Lösung auch für mathematisch exakte Punkte funktioniert.
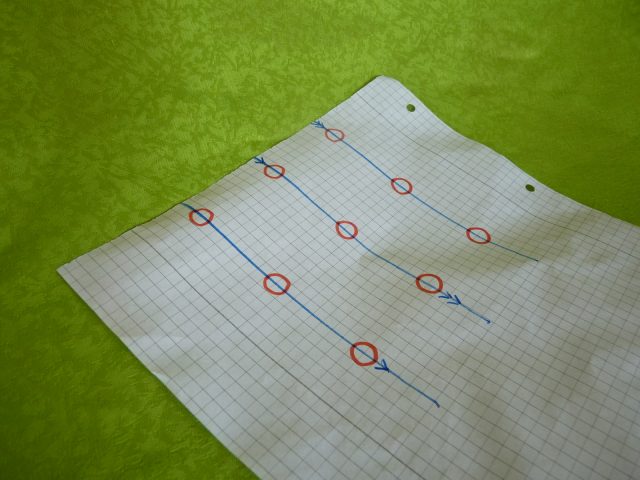
In der zweiten Dimension ist die Linie unterbrochen. Foto: ts / Epoch Times






























vielen Dank, dass Sie unseren Kommentar-Bereich nutzen.
Bitte verzichten Sie auf Unterstellungen, Schimpfworte, aggressive Formulierungen und Werbe-Links. Solche Kommentare werden wir nicht veröffentlichen. Dies umfasst ebenso abschweifende Kommentare, die keinen konkreten Bezug zum jeweiligen Artikel haben. Viele Kommentare waren bisher schon anregend und auf die Themen bezogen. Wir bitten Sie um eine Qualität, die den Artikeln entspricht, so haben wir alle etwas davon.
Da wir die Verantwortung für jeden veröffentlichten Kommentar tragen, geben wir Kommentare erst nach einer Prüfung frei. Je nach Aufkommen kann es deswegen zu zeitlichen Verzögerungen kommen.
Ihre Epoch Times - Redaktion